During 2017, I saw a lot of news articles talking about how the Evil Power Companies were being Meanie McMean by not letting people with solar panels use them when the grid was down.  The implication (in many news articles) was that these powerless people with solar panels could use them to power their home while the grid was down, if only the evil power company didn’t require that solar not work if the grid was down.  The picture painted was one of power company executives, twisting their mustaches, cackling in the glow of their coal fired furnaces, going on about how if they can’t deliver power, nobody shall have any power!

That sentiment (and those similar) is somewhere between “showing extreme ignorance of solar” and “actively misleading,” depending on the author’s knowledge of solar and how it’s typically implemented.

So, of course, I’m going to do better.  Because I can.  And because I’m sick of reading that sort of nonsense on the internet.  You will be too, after understanding the issues.

Solar Panels (Are Weird)

Any detailed understanding of solar power requires an understanding of solar panels - because they’re the power supply to the entire system.  And, in terms of the available power supplies out there, solar panels are weird.  They’re substantially different from anything else, and this impacts how you can use them for grid tied and off grid power.  The biggest problem is that they’re very easy to drive into voltage collapse (and therefore power collapse) if you draw beyond the peak power they can produce at the current temperature and illumination.

This is an example IV (current/voltage) curve out of the datasheet from my panels - it’s one I had laying around.  The numbers don’t matter, because all solar panels work this way - just with different numbers on the scales.

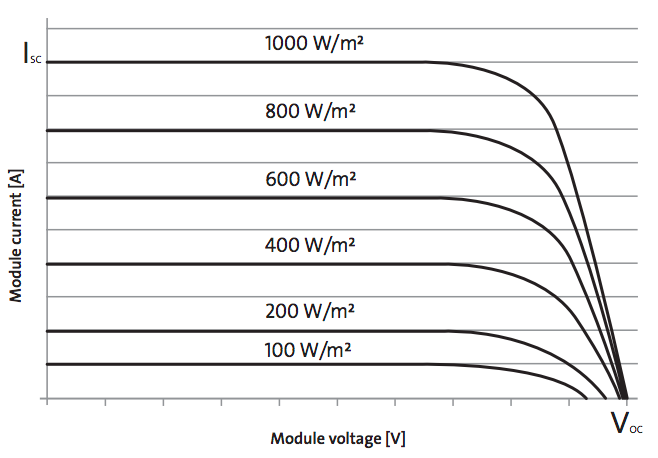
What you’re seeing, and what’s vital to understand, is that a solar panel will supply a certain current (at any voltage) - up to a certain point.  That current is directly affected by the illumination available (the different W/m^2 curves - that’s illumination power per square meter of panel area).  At a certain voltage, the current starts to drop off, and eventually you hit the open circuit voltage (Voc) - the voltage the panel produces when there’s no current draw.  The peak power (maximum power point) on the panel comes slightly past the start of the drop in voltage, and the available power drops very rapidly as you go past that point into the voltage collapse.  At both the short circuit point (0V, plenty of amps) and the open circuit voltage (0 amps, plenty of volts), the panels are producing zero usable power.

DigiKey has a great diagram that demonstrates how this works for their particular example panel.  The red curve is the current, and the blue curve is the power.  The dot represents the maximum power point on both curves.  Notice that the power curve to the right of the maximum power point is quite steep - it’s not a gentle dropoff.

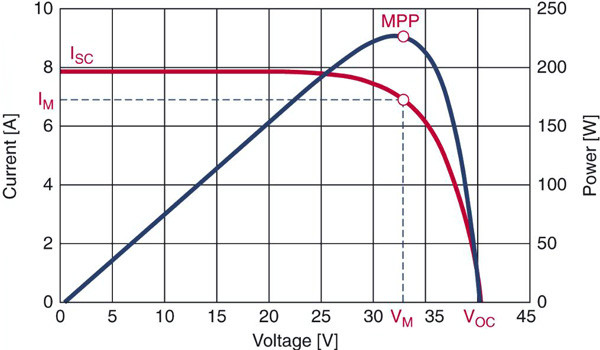
The curves change absolute values somewhat both with illumination and temperature.  A colder panel will produce a higher voltage, which a good MPPT controller can extract as extra watts in the winter (when you really want all the watts you can get).  Plus, there are curves over the standard 1000W/m^2 illumination you might see in certain conditions that lead to an awful lot of extra power.  When might you see that?  A vertical panel, with snow on the ground, on a bright, sunny winter day.  Also, “cloud edge” effects (the edge of certain cloud formations can focus more light on your chunk of ground than full sun).  In those conditions, a panel will produce more than rated current and voltage, and you’d better have designed for that!  I’ve seen north of 11A from 9A panels in the winter reflection condition.

My east facing panels, right now, are producing 1.8A at 58V. In these conditions (afternoon shade, but a partly cloudy day), they’d happily provide 1.8A at 12V, 1.8A at 24V, 1.8A at 40V, 1.8A at 60V… right up until I pass the knee in the curve. Open circuit voltage today is 70V (my little PWM controller can tell me this), so peak power is probably right about 57-60V.  And, if I were to try to pull more than 1.8A from them, the voltage would collapse. That’s just what they can do right now, aimed as they are.

Swing them around to face the sun, and they’re operating at 7.4A at 58V. These panels are connected with a PWM controller (pulse width modulation, or basically a switch that toggles quickly), so they always operate at whatever my battery bank voltage is. That means they’re producing more watts when my bank is charging heavily (60V) than empty (48V). But that’s the way I hooked them up because it’s cheap and plenty good enough for my needs.  Since their peak power comes fairly close to my battery bank voltage, the (small) gains of a MPPT controller don’t justify the cost on this secondary array.  But what’s MPPT?

MPPT: Maximum Power Point Tracking

Look back at the diagram. The top of the power curve is called the “maximum power point” - for what should be obvious reasons. That particular voltage/current point is the absolute maximum number of watts you can get out of the panel at this particular point in time. A more sophisticated charge controller can track this point by sweeping across the range of voltage/current values and finding the maximum power. My main array of 8 panels is hooked up to a MPPT charge controller (a Midnite Classic 200, which runs around $600). If I load things up enough to get them at max power point, they’re operating at about 116V/13.8A/1600W (two strings of 4 panels in series instead of one string of 2 like my morning panels). It’s a good solar day.  The MPPT controller converts that power into what my battery bank (and the rest of my system) wants - about 27A at 59V.  This is the insides of a Midnite Classic 200, and it’s a fairly complicated bit of circuitry (this unit can handle up to 4500W of panel on a 72V battery bank).  This is only doing the maximum power point tracking and DC-DC conversion - it’s not even outputting an AC waveform!

What happens when I don’t need all that power (assuming the batteries are full)? If my AC compressor is turning, I need about 1.6kW. Shut that down, I’m pulling about 950W. Where does the excess power go?  It simply doesn’t get produced in the first place.  A charge controller can restrict the energy drawn by drawing less current than the maximum power point, which lets the voltage float up towards the open circuit voltage (you could also draw more current, but that’s a far less stable way to operate).  When I’m pulling 950W, my main array is running at 133V/5.1A/678W, while my morning panels make up the rest (actually, they produce what they can, and the main array makes up the rest). The system only draws as much as is actively being used.

So, going back to the curve: If I try to draw more than whatever the peak power of my panels are (in current conditions), the voltage (and power) collapses. If I tried to pull 2A out of my morning panels when they were facing east and only able to source 1.3A, the voltage would collapse to 0V and the power would drop to zero. What if I try to pull 2A out of them when they’re swung out and able to produce 7.4A? Well, I can pull 2A for as long as I want.

The key here is that you cannot pull more than the maximum power from a panel - even by a little bit - without suffering a massive voltage and power collapse.  You can operate below the maximum power point easily enough, but it’s hard to identify the maximum power point without sweeping through the whole range to find it.

Microinverters Versus Charge Controllers/Off Grid Inverters

A typical grid tied solar system is built with microinverters.  These are a combination MPPT tracker and inverter for each solar panel, normally in the 280-320W range, though that’s creeping up with time as panel output increases.  The output from these synchronizes with the grid - typically 120VAC and 60Hz, in the US. However, they’re very simple devices. They don’t have onboard frequency generation - they can only work when given a voltage waveform to synchronize against. They also only work at maximum power point - that’s their whole point, and when the grid is up, they’re connected to what is, from the perspective of a microinverter, an infinite sink. So they sit there, finding the maximum power point, and hammering amps out onto whatever waveform the grid is feeding them.

They also, because they’re feeding the grid, have zero surge capability. A 320W microinverter can never source more than 320W, which is fine, because the panel will generally not produce more than 320W. There are conditions where it can, but they’re unlikely for roof mounted panels (a very cold, very clear winter day would seem like a case, but the panels aren’t typically aligned to take advantage of low winter sun).  When the inverter can’t process everything the panel could produce, it’s called “clipping,” and it’s really not that big a problem as long as it’s not many hours a year.

But, because of these requirements for the operating environment, microinverters are significantly cheaper to build.  They just need to be able to find max power point and shove that power onto an existing waveform.

An off grid system typically has two different devices - a charge controller (the Midnite Classic shown above) and an inverter (sometimes more than one of each in parallel).  These are separate devices, and cost a good bit more than a microinverter of comparable power.  But, they also work with the battery bank, and have to deal with more amps. A 320W microinverter will typically consume around 10A on the DC side and output about 2.5A on the AC side. My charge controller tops out around 75A on the battery side, and my inverter can pull 125A from the battery bank (peak current).  I’ve got a massive low frequency inverter that weights about 40lb (for stationary use, I consider power density in inverters an anti-feature - I’d rather have a massive inverter than a tiny one, because they tend to last a lot longer).  My inverter is rated at 2kW, but can source up to 6kW briefly if needed.

Some of the newer systems use a high voltage DC coupled setup - this is how the DC Powerwalls work (which was the Powerwall 1, and was advertised for the Powerwall 2, but then cancelled). For this, you have a very high voltage string of panels (typically 400VDC, either from panels in series or from power optimizers, which are basically a microinverter that outputs high voltage DC), the battery bank hangs on that bus, and the inverter swallows 400VDC and puts out AC.  This works better for higher power systems, but it’s not a very common off grid layout.

Batteries

You need batteries in an off grid system for two reasons: Energy storage is the obvious reason, but they also cover peak power demands. Lots and lots of things in a typical home draw far, far more startup power than they do peak power. Anything with a motor is likely to do this, and compressors are particularly bad about this (fridges, freezers, air conditioners, etc). Pretty much any semi-inductive load is going to be a pain to start in terms of current requirements.  Again, using data I have handy, my air conditioner pulls about 700W running, but it pulls somewhere around 2kW, very briefly, when starting. My system is designed for this sort of load (my inverter is a 2kW unit with a 6kW peak surge current capability), but you have to be able to handle that, or the system won’t work. If you have purely resistive loads, there’s still a startup surge - a typical bulb draws more current on starting as resistance goes up with temperature (you can radically extend the life of incandescent bulbs by putting a negative temperature coefficient resistor in series with them, and this was a popular trick with aircraft landing lights before LEDs got bright enough).  This is another reason off grid inverters tend to be large and heavy - they have to be able to provide that peak power.  Most off grid inverters have a peak power delivery of 2-3x their sustained power delivery, and mine is on the high end, peaking at 3x rated.

Worth noting on batteries: They suffer age related degradation as well as as cycle based degradation. You cannot keep any battery alive forever, even if you don’t use it. Lead acid chemistries (flooded, sealed, AGM, whatever) are rarely good past about 10 years, though if you were to keep them really cold you could probably manage it (some of the industrial cells are rated for 15 years, but they’re quite a bit more expensive). Lithium… eh.  It supposedly lasts longer, but I treat accelerated lifespan tests as a general guideline to compare batteries instead of full truth.  I make a lot of money on dead lithium, and there’s a lot of ways to kill them.  They also require heating in the winter or you’ll get lithium plating while charging (which is also a way to kill the capacity).

Let me offer a general guideline on batteries: Any time you put any sort of battery into a power system, the system will never “pay for itself.”  There may be specialty cases where this isn’t true, but it’s a solid first order approximation you should be aware of.  Off grid power is insanely expensive.

Off Grid Without Batteries

Now, how does all of this relate to off grid use without batteries?

If you have a typical grid tied system (microinverters or normal string inverters, so easily 95+% of installed rooftop solar), the system is_ technically incapable_ of running off grid (without additional hardware). There’s no waveform to sync with, and the inverters cannot produce their own waveform.  Also, they cannot operate at a reduced power output (this is more a side effect of the firmware, but it’s true of the vast majority of ones out there). So they can’t produce less power than the panels are creating at the moment, and they can’t produce more.  And they can’t make a valid AC waveform out of it.  You can see how this might be a problem.

If you want off grid capability from a microinverter system, you need what’s called an “AC coupled system.” This involves a battery bank (uh oh), and an inverter/charger that can suck power from the home’s AC grid, as well as deliver it. You generally can’t size this to use the whole roof, as a 10kW charger/inverter and a battery bank that can handle that sort of charge rate are really expensive. Basically, this system provides a waveform for the microinverters, sucks excess power, and eventually shuts the microinverters off (usually by pushing frequency out of spec for them). There theoretically exists a setup that can tell the microinverters to back off a bit, and with the newer UL specs, that should be easier with some of the improved ridethrough curves, but… it’s complex, and nobody really does this. Generally, you only couple some of the solar panels to the AC coupled setup, because it makes a smaller charger/inverter possible. So you may AC couple 4kW of a 12kW system.

The only real way to get off grid power without batteries is to go with an inverter that has an emergency outlet.  Some of the SMA inverters support this (they call it Secure Power Supply) - you feed the whole rooftop array into them, and they can, if the sun is shining, provide 1.5kW or so to a dedicated outlet - assuming there’s enough solar power. So, from an 8-10kW array, on a sunny day, you can get 1.5kW by operating well below the peak power point. If the array can’t keep up with current demand (a cloud goes over), the outlet shuts down. It’s better than nothing, but this is just about the only way you can get battery-free off grid power. To get any sort of stable battery-free power, you have to run the panels well, well below peak power (30-50% of peak is as high as you can really run), and even then, you have a horrifically unstable system. If the array power briefly drops below demand (perhaps an airplane has flown over), you shut down the entire output for a while. Hopefully your devices can handle intermittent power like this. If the array can source 1300W at the moment and a compressor tries to draw 1301W while starting, you collapse the array voltage and shut down the outlet.  That’s really hard on compressors (and everything else attached to the outlet).

If, as some nutjobs prefer, you want sustained off grid running for most of the house, you can design a system with batteries that’s intended for this sort of use. I plan to build this, eventually. I’ll have 8-12kW of panels on the roof, feeding into a few charge controllers. These will feed into a moderately sized battery bank under my house, and will be coupled to a large inverter that supports grid tied production as well as standalone use (probably an Outback Radian 8kW unit). I’ll have most of the house downstream of the inverter, so I can run everything I care about off the inverter - I’ll lose some loads like the heat pump backup coils, possibly the stove, but the rest of the house will work, and I’ll have enough surge capacity to do things like run the well pump and the air conditioner.  I don’t expect this system to ever “pay off” in financial terms, but I value stable, reliable power, and a test lab for this sort of operation.

Or you can separate your backup power from your solar, which I’ll talk about a bit later.

So… hopefully that’s a bit of a technical overview of how things work. I assure you, most of the furor over this is related to how systems are installed, not “Meanie Power Company Being Evilly Evil.”

“Islanding”

One term one will hear tossed about is the concept of “islanding.”  This refers to a chunk of the power grid (possibly a single house) that has power while the rest of the local grid is dead.  It’s common to hear “anti-islanding” blamed for why a home’s solar can’t produce power when the grid is dead.  Lineworker safety is usually mentioned in the next sentence.

What this means, simply, is that a local generating system cannot (legally) feed into a dead section of power grid.  For a home power system, this means that unless you have a specific mechanism for disconnecting the home from the power grid (typically called a “transfer switch”), you cannot power the local home circuits from solar or generator.

Now, that said, it’s really less of an issue than it’s made out to be.  Backfeeding the power grid, according to some lineworkers I’ve talked to, is really not a big concern for two reasons. First, lineworkers assume lines are live until proven otherwise.  And, second, no residential system is going to successfully backfeed a large dead section of grid.  The grid without power looks an awful lot like a dead short, so the microinverters or string inverters or generator or whatever will instantly overload and shut down. It’s in the regulations, but it’s really not that big a concern from a technical/safety perspective.

But, if you haven’t explicitly set your system up to support islanded operation with a transfer switch and battery, your solar won’t power your house with the grid down.

It’s Not Power Companies Being Evilly Evil - It’s Homeowners Being Cheap

Why have I written all this?  To explain (hopefully) that the reason most solar power systems won’t work off grid has literally nothing to do with power companies being evil and demanding that you buy their power.  It has everything to do with the system not being designed to run off grid.  Why are they designed that way?  Because it’s cheaper.  Period.  A microinverter based system is substantially cheaper than anything with batteries (which will need regular replacement), and that’s what people get installed when they want a reasonably priced bit of rooftop solar to save money on their power bill.

If you want to get a rooftop solar system that powers your home with the grid down, you can do it!  The hardware is out there.  But such a system will be significantly more expensive than a normal grid tied system, and it will likely never “pay off” in terms of money saved.  That’s all.

So stop blaming the power companies for homeowners buying a grid tied system (because it’s cheap) and then complaining when it won’t run off grid.  That’s like complaining that a Mazda 3 won’t tow a 20k lb trailer.

The Cheap Path to Backup Power

Now, if you want emergency backup power, and your goal isn’t to spend a comically large sum of money on a system like I’m designing (the ROI on my system design is “never” if you don’t value sustained off grid power use), the proper solution is a generator. I highly, highly suggest a propane (or natural gas, if you have that) generator - it’s so much easier to store propane than gasoline without it going bad. Ten year old propane is fine. Ten year old gasoline is a stinky, gummy varnish.  Says the guy with an extended run tank for his gasoline generator.

A generator and transfer switch is the right option for almost everyone interested in running through a power outage.  The solar feeds into the grid side of the transfer switch, the generator feeds into the house side.  When the power goes out, flip the transfer switch, light the generator, and go.  Or, if you get really fancy, you can get an automatic transfer switch that will even start the (expensive) generator for you!

This doesn’t give you uninterrupted power (there’s still a blip when the power sources change), but it’s far, far cheaper than putting your house on a giant inverter and adding batteries.

Can’t Microinverters Sync to a Generator?

If the microinverters need a waveform to sync with, couldn’t you create that waveform with a generator or a tiny little inverter and have the rooftop units provide the rest of the power?

Unfortunately, no.  A microinverter generally won’t sync to a generator - and if it could, it wouldn’t work anyway. Most fixed RPM generators (typically the cheaper open frame generators, running at 1800 or 3600 RPM) put out such amazingly terrible power quality that a microinverter will refuse to sync against them. Put one on a scope if you have one. They’re bad. It’s very nearly electronics abuse to run anything more complicated than a circular saw from them.

You can perhaps get the microinverters to sync against an inverter generator, but then where will the power go? Let’s say you’ve got a 3kW Honda and an 8kW array - not an uncommon setup. You start the generator, the freezers and such start up, pull 1500W. The microinverters sync, and with the sun, start trying to dump 4-5kW onto the house power lines. The Honda will back off, since it looks like a load reduction, but you’ve got 4000W of microinverter output trying to feed 1500W of load, and the microinverters won’t back off. What they’ll do is drive voltage or frequency high, shut down, and then the Honda has to pick up the 1500W load instantly. And you’ll do this over and over. If you don’t destroy the generator, you’ll probably destroy the loads. It just doesn’t work.

The AC coupled systems solve this by saying, “Well, I’ll just pull power into the battery bank until it’s full.” So they’ll let 1500W of that output from the rooftop units feed the freezers, and pull the other 2500W into the battery bank, so things are stable. And then shut down the microinverters by pushing frequency out of spec when the batteries are full.

UL 1741 SA compliant inverters might be able to be tricked into partial output, but I don’t think that’s likely to be very stable for long.

Small Scale Battery Backup

Another valid option for backup power (as pictured in the title picture) is some sort of small battery box (with or without solar).  I built a 1kWh power toolbox (with solar capability) last summer, and that can run at least some useful loads if we lose power.  Goal Zero makes some nice equipment in this realm, if somewhat pricey.  Though, really, my “power is out for a long while” plan involves my generator and some extension cords, for now.

Power Grid Stability and Rooftop Solar

While I’m on the topic of residential solar, I’d like to talk a bit about why I’m not a huge fan of it, as commonly implemented.  This often surprises people who assume I have to be massively pro-solar (based on my off grid office and how much I write about it), but I don’t think that residential rooftop solar is a particularly good idea, and I’m a far bigger fan of utility scale solar deployments (“Community Solar” and large commercial solar farms).  I’m genuinely excited to find new solar farms when I’m out flying, and they keep popping up like weeds in my area.  Most of the utility scale solar out here is single axis trackers, which help with evening out power production throughout the day (and, importantly, help with production in the morning and evening).  They’re awesome, and I’d love to tour one of the plants one of these days.  If you’re a solar company in the Treasure Valley, I promise I’ll be very impressed if you take me on a tour!

Why am I not a huge fan of rooftop solar?  I’ll dive into that shortly, but, fundamentally, rooftop solar is a bad generator.  It tends to be focused on maximizing peak production (at the cost of useful production), because the incentives are for peak kWh, not useful kWh.  And, worse, rooftop solar is a rogue generator.  The power company has no control over the production (which peaks at solar noon and goes away whenever there’s a cloud), and the power is the equivalent of sugar - empty VARs.  I think the power grid is pretty darn nifty, and I’m a huge fan of keeping it running.  Rooftop solar, as currently implemented, is really very much at odds with a working power grid.

The Grid as Your Free Battery

Typically, rooftop solar is on some variety of “net metering” arrangement.  This means that if you pump a kWh of energy onto the grid, you can pull a kWh off.  You get to use the grid as your free, perfect, seasonal battery - which is an absolutely stunning, amazing, sparkling deal for the homeowner.  No battery technology out there does this, except the power grid!

It’s kind of a crap deal for the power companies, though.  In exchange for you putting a kWh onto their grid, whenever your system happens to have some excess, you get to pull a kWh off their grid - for free - whenever you happen to need it.  This is the sort of arrangement you put in place when the only people who have rooftop solar are the kooks (say, the 80s or 90s), and you can safely ignore them.  It does NOT work well when more and more people have rooftop solar, and are demanding that the grid bend to their needs, not the needs of grid stability.  I’ll talk about this more in the grid maintenance section.

Inertia/Frequency Stability/Empty VARs/Restart Behavior

A related issue for grid stability is the lack of inertia (or synthetic inertia) in residential solar installs.  This is getting slightly better with the UL 1741 SA listed inverters, but they still only fix it in one direction.

What’s inertia, in the context of power systems?  Literally that - traditionally it’s been provided by the inertia of the large spinning generators, their turbine systems, gearboxes, etc.  Rotational inertia!  Without diving into the details, this provides the first order response to grid load changes by countering frequency changes mechanically.  If there’s a sudden spike in load (or a generation station trips off), the initial response by the grid is that the frequency tries to drop (as more power is demanded of the remaining generators).  The drop in frequency is caught by the plant throttles that add more steam (if available) to the turbines, and then the grid tries to add capacity to seek the correct frequency.

Microinverters generally don’t offer any grid stability services.  They simply match what’s present - and, worse, most of the deployed ones trip off if the frequency gets too far away from spec.  So, if the grid frequency drops from a high load situation, the inverters may trip off and reduce generation even more.  It’s a positive feedback loop, and not a good one.

This sort of stability-free generation doesn’t matter as much if there are only a few people with rooftop solar, but it’s the sort of thing that leads to emergent instability if there are a lot of people with solar.

The recent UL 1741 SA tests (and related IEEE 1547 standard updates) address this significantly by radically increasing the ride-through windows and allowing for curtailed output if the frequency or voltage is too high, but residential inverters still only operate in the “curtail output” side of the standard.  They can’t (won’t?) do something useful like operate at 80% of maximum power, so they can respond instantly to a lowered frequency on the grid by adding power.  Solar can respond nearly instantly to a load demand, but only if it’s operating below the maximum power point to start with.

But, even with those changes, there’s still the potential for some sort of emergent oscillation to arise.  At some point, there will be little enough effective inertia on some grid segments that something quite interesting will happen, and I expect rooftop inverters to be significantly at fault from how they respond to some unexpected trigger pattern.

Power Production/Duck Curve Issues

Related, rooftop solar tends to be aimed as south as possible, to maximize peak production.  That maximizes power generated, but it doesn’t maximize grid utility of the power.  Peak demand tends to be in the morning and evening, and south aimed solar doesn’t help with this.

If you’ve paid attention to solar, you’ve seen the “duck curve” in various articles.  It relates to the reduced demand on generating plants during the middle of the day, and the increasingly brutal ramp rate (rapid changes in power plant output) to deal with the increase in evening load, right as the rooftop solar is dropping off.  Since the utility has no control over individual rooftop inverters, they basically have to “just deal with it.”  This is part of why we’re seeing an increase in natural gas turbine plants - they can load follow better than other plant designs (including nuclear).

A utility scale solar plant can help resolve this in multiple ways.  Most of them tend to be on single axis trackers, which helps extend their production into the morning and evening - at the cost of peak production in the middle of the day.  In addition, a utility solar plant can bid into various grid services, can operate curtailed (less than 100% output to provide headroom for frequency stability, or to provide stable output despite clouds), and generally is far more useful to the grid than rooftop solar.  And, if you want to pair storage with it, it can behave much as a traditional power plant in terms of power bidding.

Utility Grid Costs/Maintenance

Finally, rooftop solar (with net metering) leads to a push of grid maintenance costs away from those who have rooftop solar, onto those who don’t.

Net metering, as I explained above, is using the grid as an ideal, free, battery.  And it’s the free part that causes problems.

I touched on demand charges a few months back when I looked at Tesla’s Megachargers and operating costs, but for any sort of serious load (industrial/commercial use), your power bill consists of two separate items: Energy charges, and demand charges.  Energy charges are per-kWh used, and are, by residential standards, absurdly cheap.  In the range of $0.04/kWh or less “cheap.”  But, separately, you pay demand charges - which are per kW charges, over the peak demand in the month (usually over a 15 minutes or an hour).  If you use very little energy overall, but pull 1MW for an hour, you’ll be paying out the wazoo in demand charges.

The reason for this is that energy, on the grid, is actually quite cheap.  The actual cost of a kWh on the grid is typically around $0.02-$0.04.  The rest of the rate (for residential rate schedules) is the demand charge, just woven into the per-kWh rate.  Generally, you’ll see some level at which the cost per kWh goes up, which is effectively the same as demand charges increasing (because someone who uses 2MWh/mo is going to need a bigger feed and more supporting grid hardware than someone who only uses at 200kWh/mo).

When you are producing on a residential schedule (which is what net metering effectively is), you break the assumptions bound into the rate schedule, quite to your benefit.  Someone with rooftop solar who is exporting enough to the grid to null out their bill is using the grid quite “for free,” despite making heavy use of the grid for both exporting their excess (when they happen to have it) and making up the lack (whenever the want it).

With demand charges, it would matter less, as you’d be separating out your grid use from your energy use, but right now, with net metering, the deal is this: “I’ll ship you power whenever I have surplus, you give me full rated power whenever I want it, you have no control over it, and I pay you nothing for using your power grid.”

This is not a particularly good way forward.

Closing Thoughts

Several thousand words later, hopefully you understand better why solar panels don’t magically let you use power without the grid.  And, hopefully, you can now communicate this any time you see that sort of nonsense showing up on the internet.  Or link them here.  Whichever.

If you want affordable backup power, just buy a generator and wire in a transfer switch.

Let me know in the comments if there are areas you find unclear, and I’ll attempt to clarify them.